Machine Learning--初识机器学习(Week3)

分类问题(Classification)

推测值X	X>=0.5	X<0.5
输出值 Y	1	0

这样的方法在某些情况下并不好用，因为有时候一个异常值会大大影响最后计算出的值

为了解决这样的问题，我们将公式变换一下：

$$\begin{align*}& h_\theta (x) = g ( \theta^T x ) \newline \newline& z = \theta^T x \newline& g(z) = \dfrac{1}{1 + e^{-z}}\end{align*}$$

这样的话，生成的值就会落在0~1之间，如图：

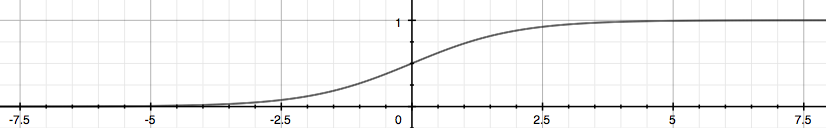
当然在概论论中:

$$\begin{align*}& h_\theta(x) = P(y=1 | x ; \theta) = 1 - P(y=0 | x ; \theta) \newline& P(y = 0 | x;\theta) + P(y = 1 | x ; \theta) = 1\end{align*}$$

那么问题来了，我们要这个hθ(x)有什么用呢？

这就引出了决策边界(Decision Boundary)这个概念了

首先对上式进行分析

$$\begin{align*}& g(z) \geq 0.5 \newline& when \; z \geq 0\end{align*}$$

Remember

$$\begin{align*}z=0, e^{0}=1 \Rightarrow g(z)=1/2\newline z \to \infty, e^{-\infty} \to 0 \Rightarrow g(z)=1 \newline z \to -\infty, e^{\infty}\to \infty \Rightarrow g(z)=0 \end{align*}$$

所以在数学计算中，我们可以这么表达：

$$\begin{align*}& \theta^T x \geq 0 \Rightarrow y = 1 \newline& \theta^T x < 0 \Rightarrow y = 0 \newline\end{align*}$$

决策边界(Decision Boundary)就是将y=1和y=0分开的那条线

Example:

$$\begin{align*}& \theta = \begin{bmatrix}5 \newline -1 \newline 0\end{bmatrix} \newline & y = 1 \; if \; 5 + (-1) x_1 + 0 x_2 \geq 0 \newline & 5 - x_1 \geq 0 \newline & - x_1 \geq -5 \newline& x_1 \leq 5 \newline \end{align*}$$

该例子中，X1 = 5就是决策边界

X1 <= 5	X1>5
Y = 1	Y = 0

当然，决策边界也可以是曲线

e.g.

$$z = \theta_0 + \theta_1 x_1^2 +\theta_2 x_2^2$$

逻辑回归模型(Logistic Regression Model)

---

Cost Function

在逻辑回归中，我们不能用和线性回归相同的那个Cost Function了，如果使用相同的，会造成输出值呈波浪状，无法收敛

逻辑回归模型的Cost Function:

$$\begin{align*}& J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0}\end{align*}$$

$$\begin{align*}& \mathrm{Cost}(h_\theta(x),y) = 0 \text{ if } h_\theta(x) = y \newline & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 0 \; \mathrm{and} \; h_\theta(x) \rightarrow 1 \newline & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 1 \; \mathrm{and} \; h_\theta(x) \rightarrow 0 \newline \end{align*}$$

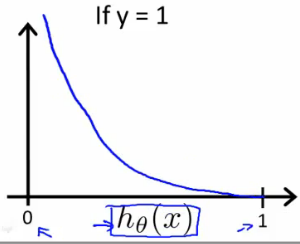
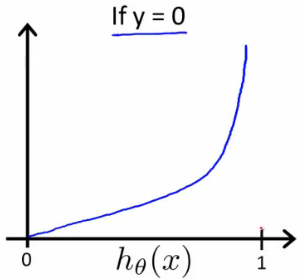
而在下式中，我们更是将这两个式子融为一体：

$$\mathrm{Cost}(h_\theta(x),y) = - y \; \log(h_\theta(x)) - (1 - y) \log(1 - h_\theta(x))$$

相应的Cost Function为：

$$J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))]$$

将其向量化之后得到：

$$\begin{align*} & h = g(X\theta)\newline & J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right) \end{align*}$$

梯度下降(Gradient Descent)

一般来说，梯度下降的方法为：

$$\begin{align*}& Repeat \; \lbrace \newline & \; \theta_j := \theta_j - \alpha \dfrac{\partial}{\partial \theta_j}J(\theta) \newline & \rbrace\end{align*}$$

计算之后，上式可化为：

$$\begin{align*} & Repeat \; \lbrace \newline & \; \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \newline & \rbrace \end{align*}$$

它的向量化表达式为：

$$\theta := \theta - \frac{\alpha}{m} X^{T} (g(X \theta ) - \vec{y})$$

更先进的算法(Advanced Optimization)

• Conjugate gradient
• BFGS
• L-BFGS

首先我们需要写一个函数来计算出与θ相关的两个量

$$\begin{align*} & J(\theta) \newline & \dfrac{\partial}{\partial \theta_j}J(\theta)\end{align*}$$

为此我们可以先写出一个返回值为它们两个的函数

function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

之后我们可以使用Matlab自带的fminunc()函数计算相关值

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

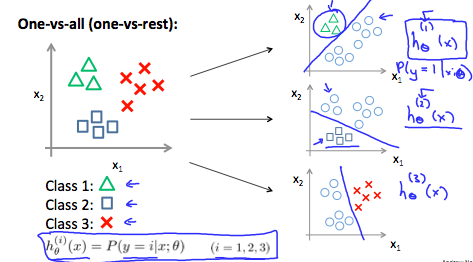
多类别分类(Multiclass Classification: One-vs-all)

---

当我们需要处理的分类问题拥有超过两种类别时，我们用y = {0,1,…,n}代替y = {0,1}

$$\begin{align*}& y \in \lbrace0, 1 ... n\rbrace \newline& h_\theta^{(0)}(x) = P(y = 0 | x ; \theta) \newline& h_\theta^{(1)}(x) = P(y = 1 | x ; \theta) \newline& \cdots \newline& h_\theta^{(n)}(x) = P(y = n | x ; \theta) \newline& \mathrm{prediction} = \max_i( h_\theta ^{(i)}(x) )\newline\end{align*}$$

其原理为：

我们在每个分类y = i中，我们将所有样本分为Xi和非Xi，并将其拓展到每个分类之中

过度拟合(Overfitting)

---

在取得预测曲线时，由于我们选取的特征变量不同，可能导致三种情况

欠拟合	正常	过拟合

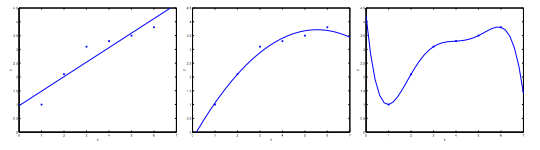
在上图中，欠拟合可能为y = θ0+θ1X

​ 正常可能为y = θ0+θ1X+θ2X²

​ 过拟合可能为y = θ0+θ1X+θ2X²+θ3X³

为解决上述问题，我们通常采用以下两种方法：

减少特征	正则化
人为选择应该留下的特征	留下所有特征，但减小其权重
利用模型选择算法	正则化在特征多且影响小时效果好

Cost Function

如果我们发现输出图像已经是过拟合了，那么我们就可以以增加它们的代价(cost)来降低它们的权重

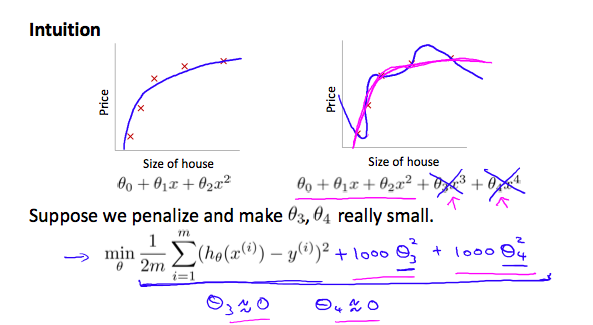
例如：

$$\theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4$$

为了减少θ3x³和θ4x⁴的影响，我们调整Cost Function为：

$$min_\theta\ \dfrac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2$$

这样在迭代时，θ3和θ4会逐渐趋于0，θ3x³和θ4x⁴的影响也会减小到一定程度

当我们拥有很多特征时，便可以将正则化θ这个任务简化为一个方程：

$$min_\theta\ \dfrac{1}{2m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\ \sum_{j=1}^n \theta_j^2$$

其中λ被称作正则化参数(Regularization Parameter)

• 当然，当λ取过大时，可能造成欠拟合

线性回归正则化(Regularized Linear Regression)

线性回归和逻辑回归，都是可以进行正则化操作的

首先我们来讲线性回归，对它来说，分为梯度下降法和正规方程法

首先，梯度下降，我们先把θ0从中分离开来

$$\begin{align*} & \text{Repeat}\ \lbrace \newline & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \newline & \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\newline & \rbrace \end{align*}$$

其中λ/m*θj代表这我们的正则化操作，同时将上者合二为一得：

$$\theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}$$

然后再用正规方程来表示线性回归

在正规方程中，我们只要加一个项就可以完成正则化了

$$\begin{align*}& \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \newline& \text{where}\ \ L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}\end{align*}$$

L是一个左上是0其余元素均为1的(n+1)*(n+1)矩阵

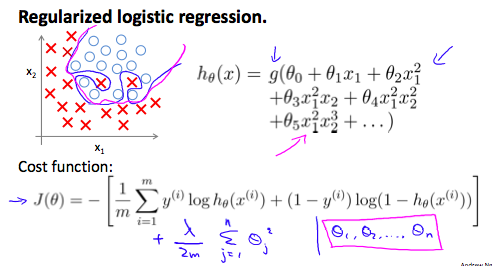
逻辑回归正则化(Regularized Logistic Regression)

通过正则化逻辑回归，我们可以有效地避免过拟合的出现，如下图，粉色的分类方法就更加科学：

Cost Function

会看一下我们之前的逻辑回归的代价函数：

$$J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)})) \large]$$

我们对此做出的调整就是在它最后加上了一项：

$$J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$$

在新加入的式子中，

$$\sum_{j=1}^n \theta_j^2$$

意味着明确地排除偏项(explicitly exclude the bias term)θ0

举个例子：如果我们有一个0到n的向量θ，该算式计算时就跳过了第0项，直接计算1到n项

因此，在计算时我们要持续地上传两个值：

赏

谢谢你请我吃糖果

支付宝

微信